3Dのショートショート その２【平行投影】

画像はクリックすると拡大されます。また略語は以下のとおりです。戻る　　　デジタル降魔録へ　　　次へ

C4d L……Cinema 4D Lite　AE……After Effects　Ai……Adobe illustrator　Ps……Photo shop
OM……オブジェクトマネージャ

【平行投影】

(マテリアルの投影法にある平行とは別物です)

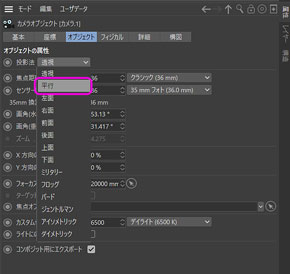
C4d Lを始めたころには知らなかったのですが、ある日、カメラオブジェクトを選択して開いた属性マネージャ中に、【投影法】という欄があることに気づきました。たくさんある割に、なんだかよく解らない設定で、切り替えてみるとカメラが映し出す映像が妙な具合になりました。それが何のためにあるのか調べることもなく、それっきり興味もわかず、ひとまず【投影法】は『透視』にしておいたのですが。

---

【補足】
　ここでいう『平行投影』はマテリアルタグの投影法にある『平行』ではなく、カメラの投影法を示しています。

---

その重要性に気づいたのは、とある依頼を受けたときでした。

　依頼内容はとても簡単なもので、正四面体に内接する球体を 3D化して、正四面体と球体がどのような状態になっているかを生徒たちに見せてあげたい。というものでした。

　そういえば、中学 3年生ぐらいに習い始める幾何学にそのようなものがあったことを記憶していまして、あ～なつかしいね。なんてつぶやいたのですが……。


　正四面体というのは正三角形を 4つ、ピラミッドのように組み上げた三角錐と呼ばれる形の一つです。ちなみにピラミッドは底が四角形なので三角錐とは別のようです。
　そんな三角錐の中にぴったり収まる球体を作っていろいろな角度から見て学習の補助にしようということでした。

　たしかに、3Dアニメーションにうってつけのものですね。もし実物の模型で作るとなると、まず三角錐は透明アクリルで作ることになるでしょうし、その中にぴったりと納まる球体も作るには大変そうです。想像するだけで、かなりの手間と費用が掛かると思われます。

　で、3Dをやり始めた ペーペー がいるからやらしてみようとなったわけです。

　確かに簡単な案件です。
　三角錐の中にぴたりと納まる球体を内接球と呼ぶ理由は、三角錐を組み立てている三角形すべての面に内部で接触している球体だから内接球です。すると必然的に球体の半径が割り出されますが、ここで求める式を書いてしまうと学習の妨げになりますのでやめておきます。とにかくやっと c4d_Lの登場です。


　指定の大きさの三角錐を作り、求めた半径の球体も作ります。ものの数分で完成です。計算したとおりに球体は三角錐の中にすっぽり収まりました。みごとにすべての三角形の面に球体の表面が触れていました。

　あらためて数学の偉大さを感じる瞬間ですね。数学や理科なんか世に出て何の役にも立たん、とよく父親に言われて育ってきましたが、それに逆らって生きてきてよかったつくづく思います。皆さんも、もっともっと夢中になれることを勉強しましょう。

　と、浮かれていられるのはここまでです。
　画面の中で鎮座する立体物を眺めてふと違和感を感じました。参考にと持ち込まれてきた書物の絵となんとなく違って見えるのです。三角形のサイズも球体のサイズもまったく問題ありませんが、カメラを通してみるとどこか変なのです。書物が間違っていると思いたいところですが、間違った絵を使う参考書なんてのもあり得ません。


　よく見比べてみると c4d_Lで作った映像のほうがこちらに迫って見えます。もっと簡単に言うとカメラに近い部分が妙に手前に見え、遠くは奥に見えます。遠近感にメリハリがあるといった感じです。

　なぜ同じものなのに見え方に違いが出るのか。

　調べてみると、これが投影法の違いによるものと理解できました。
　つまり製図や教科書紙面に掲載されている立体図などは『平行投影法』と呼ばれる方式で作られているそうです。あえて立体感を出さずに、図面としての正しい形状を求めた表現方法だそうです。

　ここでやっとつながりました。c4d_Lの投影法に『透視』以外のものがあることに。その中にちゃんと『平行』というと投影法が準備されていました。
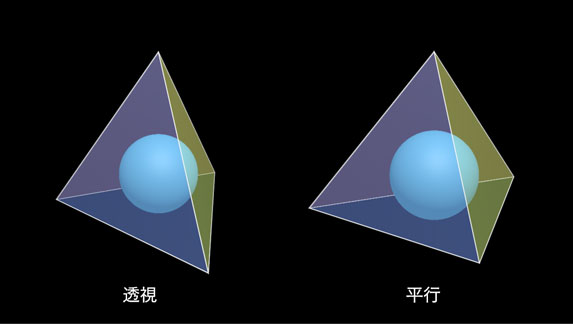
　次の写真でその違いを見てください。

　左が通常の『透視』で右が『平行』です。

右の平行投影がまさに参考書の絵と間違いなく同じものでした。

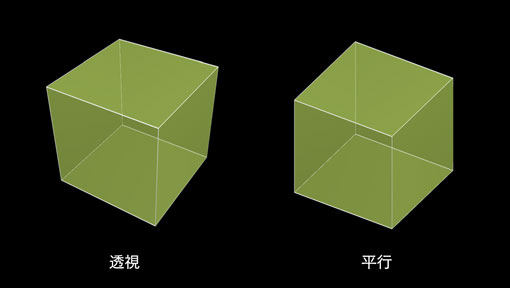
　これを立方体で比較すると、もっと顕著に現れます。

見慣れた透視投影のほうが正しい遠近感に感じますが、数学で使われる図は右の平行投影です。パースがおかしいのではなく、正確性を重視するがために、辺の長さをそろえているからですね。

　なるほど……。

　このような投影法を使用することもあるということを、また勉強したのでした。

【25】3Dのショートショート その２【平行投影】　　　終わりました

戻る　　　デジタル降魔録へ　　　次へ